P1282 多米诺骨牌
题目描述
多米诺骨牌有上下2个方块组成,每个方块中有1~6个点。现有排成行的
上方块中点数之和记为S1,下方块中点数之和记为S2,它们的差为|S1-S2|。例如在图8-1中,S1=6+1+1+1=9,S2=1+5+3+2=11,|S1-S2|=2。每个多米诺骨牌可以旋转180°,使得上下两个方块互换位置。 编程用最少的旋转次数使多米诺骨牌上下2行点数之差达到最小。
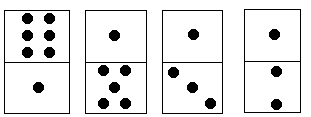
对于图中的例子,只要将最后一个多米诺骨牌旋转180°,可使上下2行点数之差为0。
输入输出格式
输入格式:
输入文件的第一行是一个正整数n(1≤n≤1000),表示多米诺骨牌数。接下来的n行表示n个多米诺骨牌的点数。每行有两个用空格隔开的正整数,表示多米诺骨牌上下方块中的点数a和b,且1≤a,b≤6。
输出格式:
输出文件仅一行,包含一个整数。表示求得的最小旋转次数。
输入输出样例
输入样例#1:
46 11 51 31 2
输出样例#1:
1
分析:
f[i][j]表示前i个牌达到j点的最少旋转次数
第i个不旋转 f[i][j]=f[i-1][j-(a[i]-b[i])]第i个旋转f[i][j]=f[i-1][j+(a[i]-b[i])]+1 就是因为前i的一部分j是由i的a[i]-b[i]贡献的取最小的例子来分析递推方程1 #include2 #include 3 #include 4 #include 5 using namespace std; 6 int a[1005],b[1005]; 7 int f[1005][12001]; 8 const int N=5010; 9 int main()10 {11 //freopen("in.txt","r",stdin);12 int n,i,j,ans,dis;13 scanf("%d",&n);14 for(i=1;i<=n;i++)15 scanf("%d%d",&a[i],&b[i]);16 memset(f,0x7F,sizeof(f));17 f[0][0+N]=0;18 //核心代码开始19 for(i=1;i<=n;i++)20 for(j=-5000;j<=5000;j++)21 {22 dis=a[i]-b[i];23 f[i][j+N]=min(f[i-1][j-dis+N],f[i-1][j+dis+N]+1);24 }25 //核心代码结束26 for(i=0;i<=5000;i++)27 {28 ans=min(f[n][i+N],f[n][-i+N]);29 if(ans<=1000)30 {31 printf("%d\n",ans);32 break;33 }34 }35 return 0;36 }
1、状态转移方程怎么写
f[i][j]表示前i个牌达到j点的最少旋转次数
第i个不旋转 f[i][j]=f[i-1][j-(a[i]-b[i])]第i个旋转f[i][j]=f[i-1][j+(a[i]-b[i])]+1 就是因为前i的一部分j是由i的a[i]-b[i]贡献的取最小的例子来分析递推方程 2、取最小的例子来分析递推方程
3、f[]的初始值被设置成多少,因为我们是求min
4、DP完后怎么取答案
5、初始值f[0][0+N]=0;
6、N的值给多少
7、数组a[-1]居然不报错
8、因为f数组初始为无穷大,只有f[0][0+N]=0;,其实有用的数据都是从f[0][0+N]=0;走出去的。
9、i是从1到n,j是从-5000到5000,j的顺序没有关系,因为都是用的上一层数据也就是i-1层的数据,其实也就f[0][0]的可用
10、用的上一层的数据的话,j的顺序是没有关系的
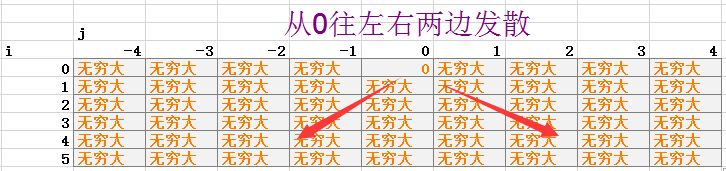
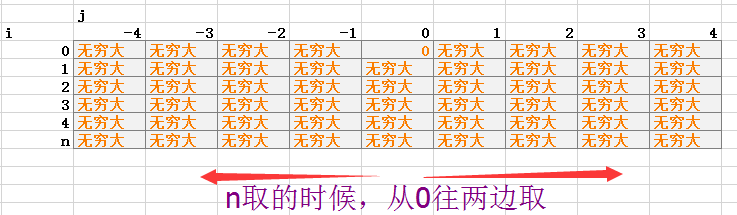
错误:
for(int j=-5000;j<=5000;j++){//改成10,忘记改回来了 f[i][j+M]=min(f[i-1][j-w[i]+M],f[i-1][j+w[i]+M]+1);//i-1写成i //漏了前面的f[i][j+M]中的M
1、第17行,i-1写成i
2、f[i][j]没有平移,忘记写+M了
3、改成10测试,忘记改回来了
这种平移的问题,一定要写好之后全部统一平移,对这题,就是遇到j的地方我给他加上M
1 #include2 const int N=1e3+10; 3 const int M=5e3+10; 4 using namespace std; 5 int f[N][12001],w[N],n; 6 7 int main(){ 8 //freopen("testdata.in","r",stdin); 9 cin>>n;10 for(int i=1;i<=n;i++){11 int a,b;12 cin>>a>>b;13 w[i]=a-b;14 }15 memset(f,0x7f,sizeof(f));16 f[0][0+M]=0;17 for(int i=1;i<=n;i++){18 for(int j=-5000;j<=5000;j++){ //改成10,忘记改回来了 19 f[i][j+M]=min(f[i-1][j-w[i]+M],f[i-1][j+w[i]+M]+1);//i-1写成i //漏了前面的f[i][j+M]中的M 20 }21 }22 for(int i=0;i<=5000;i++){23 int ans=min(f[n][i+M],f[n][-i+M]);24 if(ans<=1000){25 cout< <